Accueil Arborescence Page précédente

|
Surfaces 3D
La petite histoire Comprendre simplement Domaines de présence Son interprétation dans l'avenir Les références Mais encore … |
|
by Pepe © Accueil Arborescence Page précédente |

|
|
La petite histoire Up Page Origine, raisons, hasard |
|||||||||||||||||||||||||||||||||||||||||||||||
|
Comprendre simplement Up Page Vagues: z(x,y)=2(sin(x/2)sin(y)+cos(x/2)sin(2y)) 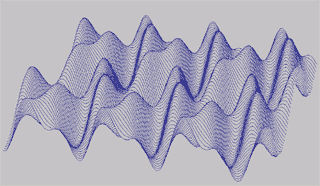
Ondulations: z(x,y)=2(sin(x/2)sin(y)+cos(x/2)sin(2y)) 
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
Domaines de présence Up Page Monde présent |
|||||||||||||||||||||||||||||||||||||||||||||||
|
Son interprétation dans l'avenir Up Page Parallélogramme 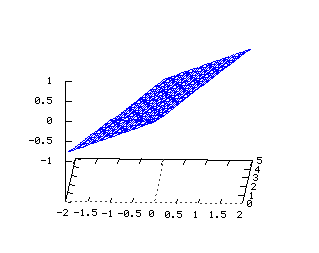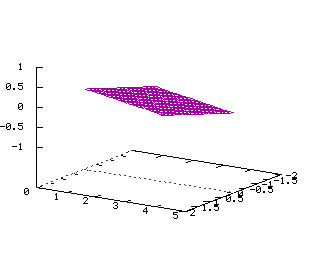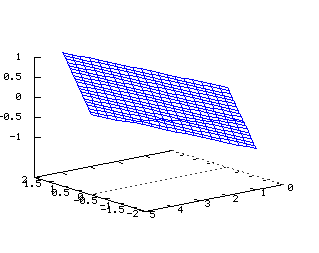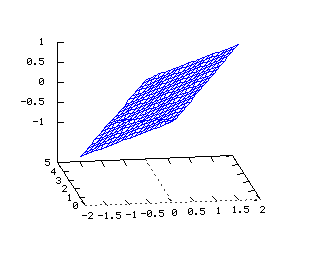 Tracé dans R3 des vecteurs
Tracé dans R3 des vecteurs
v1=(a1,b1,c1) et v2=(a2,b2,c2), au point A=(a,b,c) Equations dans R3: x=a+va1+va2 y=b+vb1+vb2 z=c+vc1+vc2 x(u,v)=2u-2v y(u,v)=4u+v z(u,v)=u-v Cone paraboloïde 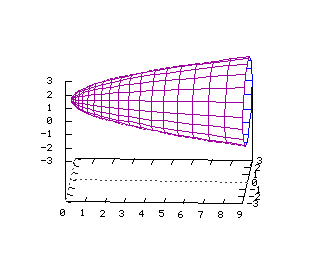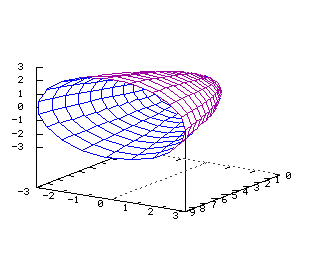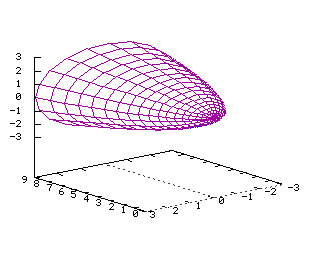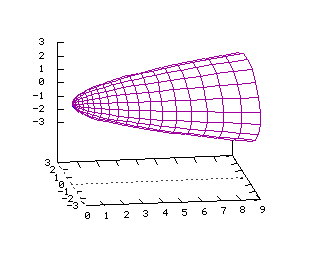 Tracé dans R3 de la surface d'équation
Tracé dans R3 de la surface d'équation
x=y2+z2 Equations dans R3: On note ici les paramètres q et r x=r2 y=r*(cos(q)) z=r*(sin(q)) x(u,v)=u2 y(u,v)=u*(cos(v)) z(u,v)=u*(sin(v)) Cone 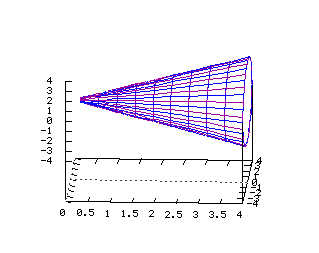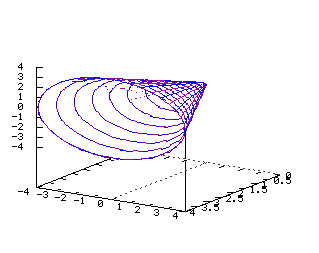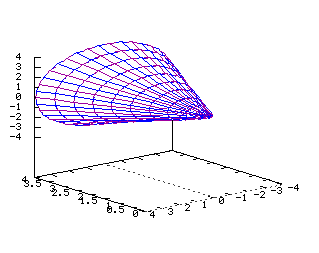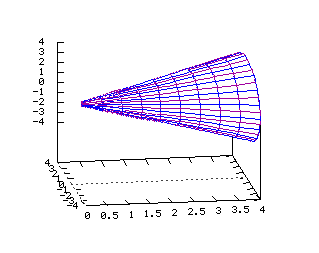 Equations dans R3:
Equations dans R3:
On note ici les paramètres q et r x=abs(r) y=r*(cos(q)) z=r*(sin(q)) x(u,v)=abs(u) y(u,v)=u*(cos(v)) z(u,v)=u*(sin(v)) Sphère 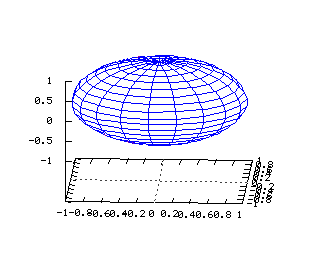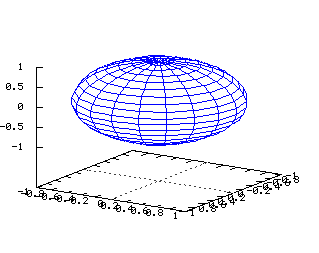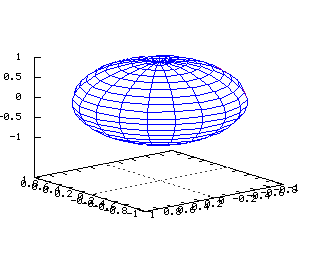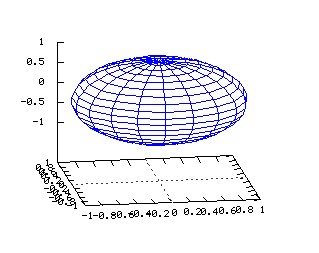 Tracé dans R3 de la surface d'équation
Tracé dans R3 de la surface d'équation
x2+y2+z2=1 Equations dans R3: On note ici les deux paramètres j et q x=(cos(j))(cos(q)) y=(cos(j))(sin(q)) z=sin(j) x(u,v)=(cos(u))*(cos(v)) y(u,v)=(cos(u))*(sin(v)) z(u,v)=sin(v) Cylindre 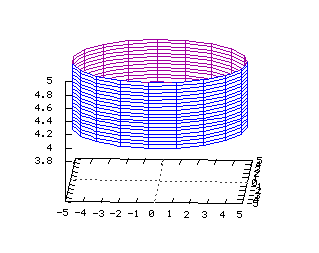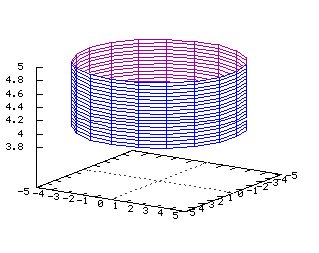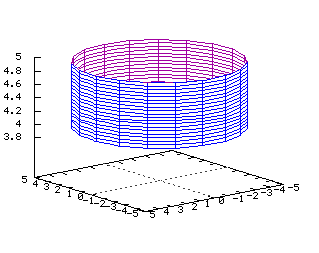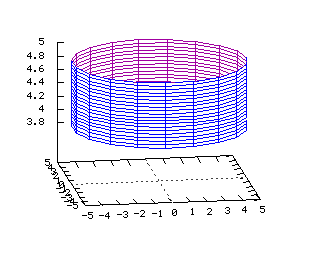 Tracé dans R3 de la surface d'équation
Tracé dans R3 de la surface d'équation
x2+y2=a2 Equations dans R3: On note ici les deux paramètres q et z x=a(cos(q)) y=a(sin(q)) z=z x(u,v)=5cos(u) y(u,v)=5sin(u) z(u,v)=v Paraboloïde  Tracé dans R3 de la surface d'équation
Tracé dans R3 de la surface d'équation
x2+y2=z2 Equations dans R3: On note ici les deux paramètres q et z x=a(cos(q)) y=a(sin(q)) z=x2+y2 x(u,v)=u*(cos(v)) y(u,v)=u*(sin(v)) z(u,v)=v2 Hélicoïde (1-y2 )(e-(x2 +y2 )/2) 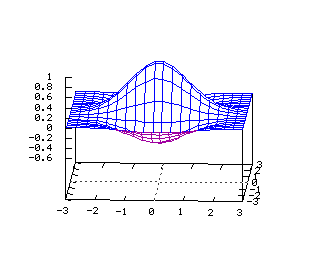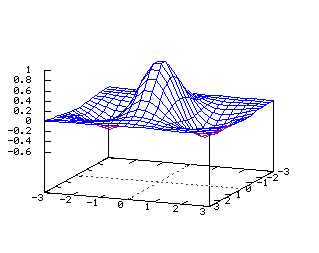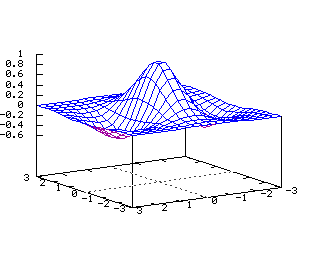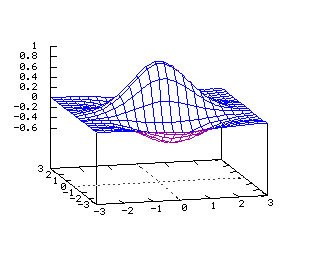
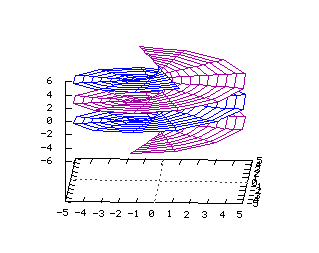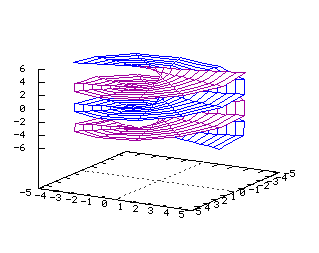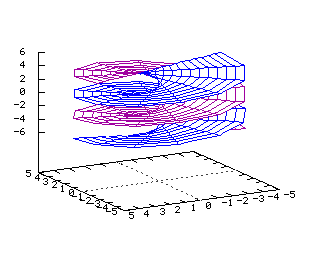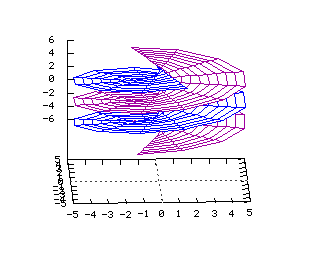 En coordonnées cylindriques:
En coordonnées cylindriques:
r=u et z=q x(u,v)=u(cos(v)) y(u,v)=u(sin(v)) z(u,v)=v Tore  Du type
Du type
x(u,v)=(A+acos(u))*(cos(v)) y(u,v)=(A+acos(u))*(sin(v)) z(u,v)=a(sin(u)) En coordonnées cylindriques: r=A+acos(j) x(u,v)=(3+2cos(u))*(cos(v)) y(u,v)=(3+2cos(u))*(sin(v)) z(u,v)=2(sin(u))
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
Les références Up Page Réseau Pepe Source Pourquoi ce site Je crois que, si les êtres humains que nous sommes ne parviennent pas toujours à évoluer comme ils le souhaiteraient _à s'épanouir professionnellement, sentimentalement et sexuellement (ce que j'appelle les trois pôles d'intérêts) c'est parce qu'il y a des barrages qui entravent leur désir d'accéder à un rêve inachevé. Je pars du principe que tout est possible, à condition de s'entourer de gens qui nous poussent à croire en nous. Contribuer au Réseau Pepe Ce site est avant tout une encyclopédie ouverte à l'imagination et au savoir, où chacun(e) d'entre vous peut participer. Si vous avez envie de partager une passion, ou si vous sentez le besoin de vous exprimer sur un point précis, je vous invite à m'adresser un e-mail (adresse électronique accessible sur ma page d'accueil). |
|||||||||||||||||||||||||||||||||||||||||||||||
|
Mais encore … Up Page Ce que vous avez toujours voulu savoir |