A la poursuite du nombre pi Formes géométriques particulières Suite infinitésimale Ö2 à la recherche des décimales Akira Haragushi et Yasumasa Kanada Les références Nombre transcendant

by Pepe © Accueil Arborescence Page précédente

© π=3,14159 26535 89793 23846 ...

La petite histoire Up Page Formes géométriques particulières 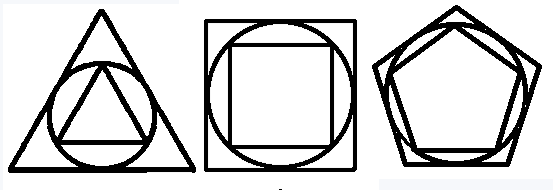Depuis l'Antiquité, les mathématiciens tentent d'aller au "bout" du nombre, sans jamais y parvenir. La Bible donne une première approximation du tour d'un cercle. Pour les Anciens, le périmètre du cercle de rayon 1 valait 3. Le cercle d'Archimède Dans le dessin de gauche, le périmètre du polygone inscrit dans le cercle est plus petit que la circonférence; la détermination de ce périmètre permet ainsi de minorer la valeur de π. Dans le dessin de droite, le polygone est circonscrit, son périmètre majore π. La plus ancienne méthode de détermination de π est due à Archimède. L'idée consiste à approcher la circonférence du cercle par un ligne brisée polygonale formant un polygone régulier. Historiquement, Archimède est parti d'hexagones, pour lesquels le périmètre de l'hexagone inscrit est de 3 et celui de l'hexagone circonscrit de 23. En doublant le nombre de côtés des hexagones, Archimède obtient des docédagones (polygones à 12 côtés) inscrit et circonscrit, dont il exprime les périmètres à partir de ceux des hexagones. Cela fait, il double un nouvelle fois le nombre de côtés, pour obtenir successivement des polygones à 24, 48 et enfin 96 côtés (il n'est pas allé plus loin sans doute satisfait qu'il était d'avoir suffisamment illustré l'efficacité de sa méthode). Archimède parvient ainsi à encadrer le nombre pi entre 3,140 et 3,143.

Comprendre simplement Up Page Suite infinitésimale Avec les progrès des mathématiques, à partir de la Renaissance, la recherche reprend de plus belle. L'arrivée de l'analyse, au 17e siècle, permet d'utiliser les notions d'infinitésimaux. On crée des séries, des suites qui possèdent une infinité de termes. On trouve alors des formules infinies pour p . Comme par exemple la série : p / 4 = 1- 1/ 3 + 1/ 5 - 1/ 7 + 1/ 9..... (et ainsi de suite jusqu'à l'infini). pi peut donc s'écrire comme le résultat d'un calcul, même s'il est infini !

Domaines de présence Up Page Ö2 à la recherche des décimales p est le nombre irrationnel dont on connaît le plus grand nombre de décimales: plus de mille milliards. Mais les mathématiciens ne battraient pas ce type de record s'ils ne s'intéressaient pas tout autant à un nombre moins prestigieux: Ö 2.

Son interprétation dans l'avenir Up Page Akira Haragushi et Yasumasa Kanada Le 02 juillet 2005, un psychiatre japonais, Akira Haragushi, pulvérisait un étrange record: en 13 heures, il récitait par coeur, et dans l'ordre, les 83 431 premières décimales de π. Puis, avec le 20e siècle et la naissance de l'informatique, les calculs vont de plus en plus loin. Les ordinateurs utilisent les formules infinies pour sonder les profondeurs du nombre. Le dernier record, qui date de juin 1997, a été obtenu par un chercheur japonais, Yasumasa Kanada. Ce mathématicien - aidé de son ordinateur - a réussi, en septembre 1999, à calculer 206 158 430 000 décimales de p, pour atteindre en 2002 les 1 241,1 milliards de décimales. Nombre de décimales de π et deÖ2 Adrian Anthoniszoon (1527-1607): π=355/113 à six décimales près; Viète en 1593: π à neuf décimales près; Adrien van Rooman (1561-1615): en 1593 π à quinze décimales près; Ludolf van Ceulan (1539-1610): en 1596 π à vingt décimales près; Ludolf van Ceulan (1539-1610): en 1615 π à trente-deux décimales près; Ludolf van Ceulan (1539-1610): en 1610 π à trente-cinq décimales près; Abraham Sharps (1651-1742): π à soixante-douze décimales près; John Machin (1680-1762): en 1706 π à cent décimales près; Français de Lagny (1660-1734): en 1717 π à cent-vingt-sept décimales près; Vega (1754-1802): en 1794 π à cent-quarante décimales près; Schulz von Starssnitzky (1803-1852): en 1847 π à 248 décimales près; William Rutherford: en 1853 π à 440 décimales près; Richter: en 1855 π à 500 décimales près; Ferguson: en 1946 π à 620 décimales près; Ferguson: en 1947 π à 710 décimales près; Ferguson: en 1947 π à 808 décimales près; 1949: π (2 035) et Ö2 (1 542) 1967: Ö2 (14 000) 1971: π (500 000) et Ö2 (1 000 000) 1973: π (1 001 250) 1997: π (51 milliards) et Ö2 (137 milliards) 1999: π (206 158 430 000) 2002: π (1 24,1 milliards)

Les références Up Page Réseau Pepe Cybersciences Recherche décembre 2005 n°392 Science & Vie février 1973 n°665 Pourquoi ce site Je crois que, si les êtres humains que nous sommes ne parviennent pas toujours à évoluer comme ils le souhaiteraient _à s'épanouir professionnellement, sentimentalement et sexuellement (ce que j'appelle les trois pôles d'intérêts) c'est parce qu'il y a des barrages qui entravent leur désir d'accéder à un rêve inachevé. Je pars du principe que tout est possible, à condition de s'entourer de gens qui nous poussent à croire en nous. Contribuer au Réseau Pepe Ce site est avant tout une encyclopédie ouverte à l'imagination et au savoir, où chacun(e) d'entre vous peut participer. Si vous avez envie de partager une passion, ou si vous sentez le besoin de vous exprimer sur un point précis, je vous invite à m'adresser un e-mail (adresse électronique accessible sur ma page d'accueil).

Mais encore … Up Page Nombre transcendant Au delà des records, le nombre pi continue d'intriguer les mathématiciens. On sait aujourd'hui que π est irrationnel, c'est-à-dire qu'il ne peut s'écrire sous la forme d'une fraction de deux nombres entiers. Il est aussi transcendant : il n'est solution d'aucune équation algébrique à coefficients rationnels, ce qui signifie qu'il n'existe aucune formule finie qui permette de calculer le nombre avec justesse. Les mathématiciens se demandent aujourd'hui si pi est un nombre aléatoire, c'est-à-dire si dans la suite de chiffres qui représentent les décimales de π, il existe une loi capable de prévoir les décimales suivantes, ou si les chiffres suivent un ordre parfaitement aléatoire. Les chercheurs espèrent trouver un motif récurent dans la suite de chiffres, un cycle de nombres qui reviendrait régulièrement, ou un chiffre plus rare que certains autres. Mais cette dernière quête n'a pas encore abouti. "Il y a trois constantes 'naturelles' qui sont vraiment à part: π, e (la base des logarithmes népériens) et Ö 5. L'exponentielle et π sont liées par la célèbre formule établie par Euler:eiπ=-1. Quant à Ö 5, on la retrouve par le biais du nombre d'or. Presque toutes les choses les plus intéressantes en théorie des nombres sont liées à l'une de ces trois constantes." Simon Plouffe, ingénieur système, consultant pour une société d'informatique, à Lyon.