Accueil Arborescence Page précédente
© Spirale d'Ulam
|
Ordonnés, sont les nombres premiers
Un ordre dans le chaos Pierre De Fermat Conjecture de Pradeep Kumar Spirale d'Ulam Les références Hypothèse de Riemann Fonction ζ (zéta) Conjecture de Golbach |
|
by Pepe © Accueil Arborescence Page précédente |
|
© Spirale d'Ulam
|
|
La petite histoire Up Page
Un ordre dans le chaos Les nombres premiers sont les unités de base des nombres entiers. Ce sont des nombres divisibles uniquement par un ou par eux-mêmes (la liste infinie débute par 2, 3, 5, 7, 11, 13, 17, etc.) Mais en dépit de la simplicité d'une telle définition, personne n'a jamais déterminé la façon dont sont distribués ces nombres parmi la suite des entiers. Le problème a toujours intrigué les mathématiciens, qui s'y penchent de plus belle ces dernières années car les nombres premiers sont couramment utilisés en cryptographie et sont devenus très utiles pour sécuriser les données échangées sur des réseaux virtuels.
|
|
Comprendre simplement Up Page
Pierre De Fermat Au 17e siècle arrive Pierre de Fermat va considérablement faire avancer la théorie des nombres. Il prouve ce qu'on appelle aujourd'hui "le petit théorème de Fermat". Si p est premier, alors pour tout a entier, on a ap = a (modulo p), (c'est-à-dire ap = a ou a + p, ou a + 2p, ..., a + np, avec n un nombre entier). Ce théorème est à la base de nombreux résultats en théorie des nombres, et il est encore utilisé aujourd'hui dans les programmes informatiques pour déterminer si un nombre est premier ou non.
|
|
Domaines de présence Up Page
Conjecture de Pradeep Kumar Pradeep Kumar et ses collègues ont découvert de l'ordre dans la distribution de ces nombres dont la particularité est de n'être divisibles que par un et par eux-mêmes. Les physiciens ont travaillé sur les différences d'intervalles entre deux nombres premiers consécutifs, aussi appelées incréments. Concrètement, la suite des nombres premiers débute par 2, 3, 5, 7, 11, 13, 17, etc. (le chiffre 1 n'est pas premier par définition). Les intervalles entre ces nombres sont ici 1, 2, 2, 4, 2, 4, etc. Les incréments sont donnés par les différences entre intervalles successifs, soit ici 1, 0, 2, -2, 2, etc. Après avoir passé en revue des milliers de nombres premiers successifs, les physiciens américains ont conjecturé que ces incréments suivent un schéma précis, avec des périodes d'oscillations prévisibles. Deux incréments successifs, par exemple, alternent souvent une valeur positive et sa valeur opposée.
|
|
Son interprétation dans l'avenir Up Page
Spirale d'Ulam
x -x-99-98-97-96-95-94-93-92-91 @-----------@-----------------|
| | | |
x 65-64-63-62-61-60-59-58-57 90 | |-----------@-----@-----| |
| | | | | | | |
x 66 37-36-35-34-33-32-31 56 89 @ | @-----------------@ | @
| | | | | | | | | | | |
x 67 38 17-16-15-14-13 30 55 88 | @ | @-----------@ | | |
| | | | | | | | | | | | | | | |
x 68 39 18 5--4--3 12 29 54 87 | | | | @-----@ | @ | |
| | | | | | | | | | | | | | | | | | | |
x 69 40 19 6 1--2 11 28 53 86 | | | @ | --@ @ | @ |
| | | | | | | | | | | | | | | | | |
x 70 41 20 7--8--9-10 27 52 85 @ | @ | @--------| | | |
| | | | | | | | | | | | | |
x 71 42 21-22-23-24-25-26 51 84 | @ | |-----@--------| | |
| | | | | | | | | |
x 72 43-44-45-46-47-48-49-50 83 @ | @-----------@--------| @
| | | | | |
x 73-74-75-76-77-78-79-80-81-82 | @-----------------@--------|
| |
x--x--x--x--x--x--x--x--x--x--x... |-----@------------------------...
|
|
Les références Up Page
Réseau Pepe Cybersciences Recherche décembre 2005 n°392 Pourquoi ce site Je crois que, si les êtres humains que nous sommes ne parviennent pas toujours à évoluer comme ils le souhaiteraient _à s'épanouir professionnellement, sentimentalement et sexuellement (ce que j'appelle les trois pôles d'intérêts) c'est parce qu'il y a des barrages qui entravent leur désir d'accéder à un rêve inachevé. Je pars du principe que tout est possible, à condition de s'entourer de gens qui nous poussent à croire en nous. Contribuer au Réseau Pepe Ce site est avant tout une encyclopédie ouverte à l'imagination et au savoir, où chacun(e) d'entre vous peut participer. Si vous avez envie de partager une passion, ou si vous sentez le besoin de vous exprimer sur un point précis, je vous invite à m'adresser un e-mail (adresse électronique accessible sur ma page d'accueil).
|
|
Mais encore … Up Page
Hypothèse de Riemann Les nombres premiers _divisibles par 1 et par eux-mêmes_ jouent un rôle central en arithmétique. Bien que la répartition de ces nombres ne semblent obéir à aucune règle, elle est étroitement liée au comportement d'une fonction découverte par le génie suisse Leonhard Euler au XVIIIième siècle. En 1859, Bernhard Riemann affirme que les valeurs intéressantes qui annulent cette fonction d'Euler se situent toutes sur une même droite. Cette hypothèse a été vérifiée pour les 1 500 000 000 premières valeurs mais jamais démontrée... Juin 2004, Louis de Branges de Bourcia, professeur de mathématiques à l'Université de Purdue, aux Etats-Unis, a annoncé avoir démontré l'hypothèse de Riemann, un problème mathématique considéré comme l'un des plus importants du siècle.
|
|
Ce que vous avez toujours voulu savoir Up Page
Fonction ζ (zéta) 
Déterminer si, oui ou non, les seules valeurs s pour
lesquelles la fonction ζ(s)=
1/2s+1/3s+1/4s+ ...
est égale à zéro sont de "partie
réelle égale à 1/2" (à
quelques exceptions près, que l'on connaît et qui
peuvent être négligées).
Il y a des liens assez complexes entre les nombres premiers, les nombres de Bernouilli et π. Les nombres de Bernouilli s'expriment avec π: π s'exprime avec les nombres premiers; la fonction ζ (zéta), qui, d'après l'hypothèse de Riemann, donne la répartition des nombres premiers, s'exprime avec les nombres de Bernouilli. Les nombres de Bernouilli déterminent les coefficients du polynôme par rapport à m: 1+2n+3n+4n+ ... + (m-1)n. La constante d'Apéry ζ, est la somme des inverses des cubes, c'est-à-dire1/13+1/23+1/33+ ... Ce nombre irrationnel doit à Euler, en 1736, sa première occurence. C'est Roger Apéry, en 1979, qui lui donna sa dernière touche. ζ(3)=1,20205 69031 59594 28539 ...
|
|
Ce que vous avez toujours voulu savoir Up Page
Conjecture de Golbach Les mathématiciens tentent depuis des siècles de trouver des règles qui situeraient les nombres premiers parmi tous les nombres entiers. Mais jusqu'à aujourd'hui, aucune règle n'a été dégagée. Plusieurs conjectures attendent encore d'être démontrées. Comme la conjecture de Golbach, qui stipule que chaque entier supérieur à 2 peut s'écrire comme somme de deux nombres premiers. Des questions restent en suspens, comme l'interrogation sur l'infinité des nombres premiers de la forme n + 1. Bref, les nombres premiers n'ont pas fini de faire chercher les mathématiciens. Conjecture de Poincar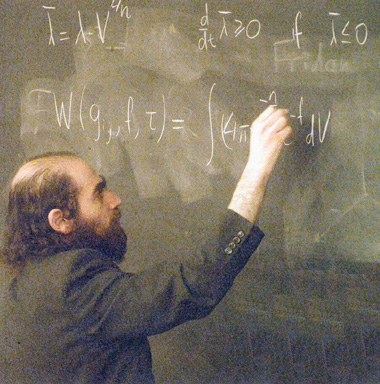é 
Grigori Perelman est né à
Saint-Pétersbourg en 1966. Après son doctorat
à l'université de Leningrad, il
intègre l'institut de mathématiques Steklov, puis
passe par New York et Berkeley, en Californie, à la fin des
années 1980. Il revient à
Saint-Pétersbourg au début des années
1990 et s'isole du monde jusqu'à la publication, en
2002-2003, de ses articles sur la conjecture de Poincaré. il
refuse la reconnaissance de ses pairs. Déjà, en
1990, il avait décliné le prix que la
Société européenne de
mathématiques lui avait décerné. En
août 2006, il a refusé la médaille
Fields, l'équivalent du prix Nobel pour les
mathématiciens. Il refusera probablement aussi le million de
dollars que voudrait lui offrir la fondation Clay pour la
résolution de ce très difficile
problème de topologie.
C'est au printemps 2003 que Grigori Perelman a présenté ses résultats lors d'une unique (et restreinte) tournée de conférences aux Etats-Unis (ici à l'université de New York).
|