Accueil Arborescence Page précédente
© φ=(1+Ö5)/2= 1,61803 39887 49894 84820 45868 34365 6...
|
Nombre d'Or
La petite histoire Comprendre simplement Domaines de présence Son interprétation dans l'avenir Les références Mais encore … |
|
by Pepe © Accueil Arborescence Page précédente |
|
© φ=(1+Ö5)/2= 1,61803 39887 49894 84820 45868 34365 6... |
|
La petite histoire Up Page Origine, raisons, hasard Le nombre d'or se retrouve un peu partout dans les arts : peinture, sculpture, musique, ... Le Parthénon d'Athènes, construit au cinquième siècle avant Jésus-Christ, est tel que ses dimensions s'insèrent dans un rectangle d'or. "Le Nombre d'Or est intéressant à étudier. La lettre Grecque φ (Phi) le désigne en hommage au sculpteur Grec Phidias (né en 490 et mort vers 430 avant JC) qui décora le Parthénon à Athènes. C'est Théodore Cook qui introduisit cette notation en 1914." Nguyên Ngoc Châu, JJR 62, Octobre 2004. |
|
Comprendre simplement Up Page Vulgarisation, de 7 à 77 ans |
|
Domaines de présence Up Page Monde présent |
|
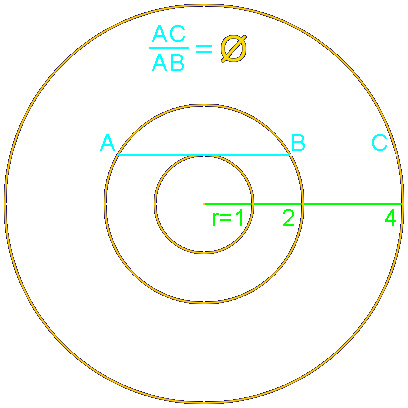
Son interprétation dans l'avenir Up Page Divine proportion Supposons que x et 1 sont les longueurs des segments AC et CB respectivement. Nous obtenons par voie de conséquence l'équation du second degré suivante: x²-x-1=0 La solution positive est le nombre d'or; il est représenté par la lettre grecque Ø (phi); la solution négative est notée Ø'. Rappelons que les solutions, ou racines, d'une équation du second degré de coefficients a, b et c sont telles que leur somme est égale à (- b/a) et leur produit et égal à (c/a). Il s'ensuit que : De ces deux égalités nous en déduisons facilement que : Ø - 1 = 1/Ø, c'est-à-dire que Ø est un nombre qui, lorsqu'on lui enlève 1, devient son propre inverse. Formule de Binet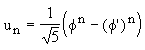 
Une formule, dite formule de Binet (1786-1856), donne directement
le n ième terme de
la suite de Fibonacci; elle fait intervenir le nombre d'or.
|
|
Les références Up Page Réseau Pepe Recherche décembre 2005 n°392 Pourquoi ce site Je crois que, si les êtres humains que nous sommes ne parviennent pas toujours à évoluer comme ils le souhaiteraient _à s'épanouir professionnellement, sentimentalement et sexuellement (ce que j'appelle les trois pôles d'intérêts) c'est parce qu'il y a des barrages qui entravent leur désir d'accéder à un rêve inachevé. Je pars du principe que tout est possible, à condition de s'entourer de gens qui nous poussent à croire en nous. Contribuer au Réseau Pepe Ce site est avant tout une encyclopédie ouverte à l'imagination et au savoir, où chacun(e) d'entre vous peut participer. Si vous avez envie de partager une passion, ou si vous sentez le besoin de vous exprimer sur un point précis, je vous invite à m'adresser un e-mail (adresse électronique accessible sur ma page d'accueil). |
|
Mais encore … Up Page Ce que vous avez toujours voulu savoir |