Accueil Arborescence Page précédente

|
Fractales
La petite histoire Comprendre simplement Domaines de présence Son interprétation dans l'avenir Les références Mais encore … |
|
by Pepe © Accueil Arborescence Page précédente |

|
|
La petite histoire Up Page Origine, raisons, hasard Un homme se promène le long d'une côte très escarpée. A la fin de son parcours, il a effectué un trajet de cinq kilomètres. Mais si, à la place de l'homme, une souris se met à suivre la côte à son tour, elle effectuera un trajet un peu plus long. Car chaque rocher que l'homme parvient à enjamber sera en fait contourné par l'animal. Et si, à la place de la souris, c'était une fourmi qui suivait la côte? La distance parcourue par la fourmi serait encore plus longue. En fait, la longueur d'une côte n'est tout simplement pas mesurable, car elle est trop escarpée. |
|
Comprendre simplement Up Page Vulgarisation, de 7 à 77 ans 
 La géométrie des fractales est née de cette constatation.
Dans les années 60, le mathématicien Benoît Mandelbrot se
rend compte que la géométrie euclidienne, qui transforme les éclairs
en des droites, les nuages en des sphères, ou les côtes terrestres
en des courbes lisses, ne transmet qu'une vision très approximative des
contours naturels. Mandelbrot décide alors d'inventer une nouvelle géométrie
qu'il veut beaucoup plus représentative de la réalité. Il
la baptise la géométrie
"fractale".
La géométrie des fractales est née de cette constatation.
Dans les années 60, le mathématicien Benoît Mandelbrot se
rend compte que la géométrie euclidienne, qui transforme les éclairs
en des droites, les nuages en des sphères, ou les côtes terrestres
en des courbes lisses, ne transmet qu'une vision très approximative des
contours naturels. Mandelbrot décide alors d'inventer une nouvelle géométrie
qu'il veut beaucoup plus représentative de la réalité. Il
la baptise la géométrie
"fractale".
Quelles sont les caractéristiques d'une fractale ? Observons un chou-fleur. Chaque branche ressemble au chou-fleur tout entier. Et à l'intérieur de chaque branche, chaque sous-branche ressemble également au chou-fleur entier... On pourrait continuer de décortiquer ainsi le légume en découvrant à chaque fois de nouveaux petits choux-fleurs à l'intérieur des branches. Dans la nature, le motif ne se répète pas indéfiniment, mais en mathématiques, rien n'empêche de créer des profondeurs infinies à un objet fabriqué par notre imagination. Ainsi, les fractales de Mandelbrot sont des figures mathématiques réalisées à partir d'un même motif (ou plusieurs) répété une infinité de fois à l'intérieur de lui-même. |
|
Domaines de présence Up Page Le monde en 2,7 dimensions Qu’y a-t-il de commun entre nos poumons, le béton high-tech et certains murs antibruit sur le bord de l’autoroute ? Réponse: "l’éponge de Menger". Il s’agit d’un concept mathématique tout droit sorti de l’imagination féconde d’un certain Karl Menger (1902-1985), un mathématicien américain d’origine autrichienne. Sa forme n’est pas sans rappeler celle de son homonyme ménager : un cube percé d’une multitude de pores, tous connectés les uns aux autres. Une curiosité née au début du siècle, qui inspire aujourd’hui pneumologues, constructeurs d’automobiles ou encore compagnies de travaux publics. A l’origine de ce pavé poreux, une recherche de l’impossible. Peut-on obtenir une surface infinie dans un volume fini ? Oui, a répondu le mathématicien viennois. Si l’on considère un cube, la superficie qui lui est associée est celle des six côtés qui le composent. A volume plus grand, surface plus étendue, l’argument semble entendu. Comment augmenter l’une sans toucher à l’autre ? Karl Menger propose une recette infaillible: si l’on partage chacune des arêtes en trois parties égales, chaque face sera formée d’un damier de neuf carrés. Commençons par vider celui du milieu. En ajoutant les parois de cette partie évidée, la superficie de la structure est plus grande que celle du cube d’origine. De ce fait, nous augmentons la surface, sans faire varier le volume... Continuons l’opération: chacun des huit carrés restants est divisé en un minuscule damier de neuf, dont la figure centrale est à nouveau évidée... et ainsi de suite, jusqu’à atteindre des portions microscopiques. 
A force de creuser dans le volume de départ, la surface ne cesse d’augmenter, certes d’une quantité de plus en plus petite, mais... sans aucune limite. Au final, c’est une dentelle tridimensionnelle qui ne déborde pas du cube d’origine. La dimension d’un tel objet ne peut pas être un nombre entier (1, 2 ou 3), elle est comprise entre 2 et 3... De la même manière, la trouvaille de Menger, scrutée sous toutes les coutures, accuse une dimension de 2,7. Au début des années 1970, Benoît Mandelbrot, mathématicien français d’origine polonaise, donne une dimension nouvelle à ces différentes démarches en les intégrant dans une théorie globale, dite des "fractales" (du latin fractus, brisé). Celles-ci foisonnent dans la nature, depuis la structure en double hélice des brins d’ADN jusqu’aux montagnes ou encore la côte naturelle de Bretagne, une ligne de faille, un nuage, un fleuve ou la répartition des galaxies. En outre, ces objets présentent une autre particularité : leur autosimilarité. Chaque partie a une structure semblable à celle de l’ensemble, exactement comme si un détail représentait, à une plus petite échelle, la totalité. Le chou-fleur en est une bonne illustration. Les échanges entre deux milieux biologiques séparés par une membrane sont également conditionnés par la surface de contact. Commence alors la deuxième vie des fractales: les physiciens s’en sont emparés pour inventer des objets de la vie quotidienne, améliorer le rendement d’une foule d’autres et comprendre le fonctionnement de certains organes humains comme les poumons. Les alvéoles pulmonaires sont l’exemple type de structure fractale. Elles présentent une très grande surface pour un volume limité : en étudiant les lois de la diffusion à travers une surface aussi irrégulière, l’équipe tente de comprendre l’oxygénation du sang. Autre application étonnante : les gratte-ciel. Des tours de 500 mètres de hauteur pourront être érigées grâce à un ciment de structure fractale, imaginé au sein du laboratoire PMC par Jean-Pierre Korb et développé par le groupe des Ciments Lafarge. « Un béton traditionnel a des grains de différentes tailles et peut supporter 30 MPa, c’est-à-dire le poids de 3 millions de kilos par mètre carré. Un critère qui détermine l’épaisseur d’un pont, par exemple », précise le chercheur. Le béton dit "de poudre réactive" - la toute dernière nouveauté - peut résister à plus de dix fois cette charge... Le secret de ce matériau hyper résistant ? Sa structure fractale : les grains qui le composent ont tous la même taille, ce qui lui octroie la propriété de présenter la même forme à différentes échelles. Avec ce béton high-tech, place aux ouvrages d’art effilés comme des lames d’acier tendues entre deux rives et aux gratte-ciel susceptibles de s’élever à des hauteurs dix fois supérieures à celles de nos bâtiments d’aujourd’hui. Les fractales n’ont pas fini d’enflammer l’imagination des mathématiciens et des physiciens. |
|
Son interprétation dans l'avenir Up Page Courbe de Von Koch 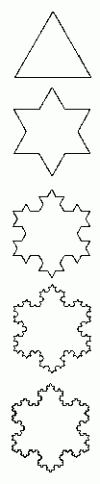 Historiquement, la première fractale mathématique est la courbe
de Von Koch. Elle a été dessinée au début du siècle,
avant même d'être baptisée « fractale ». La courbe
est très simple à construire. Il suffit de dessiner un triangle
équilatéral (trois côtés de même longueur). Chaque
côté du triangle est divisé en trois tiers. Le tiers du milieu
sert de base à un nouveau triangle équilatéral, puis il est
effacé. On recommence la procédure sur chaque nouveau côté...
et ainsi de suite jusqu'à l'infini. La courbe est fermée, c'est-à-dire
qu'elle ne possède pas de « bouts » libres, et pourtant elle
est de longueur infinie ! Une bien étrange propriété...
Historiquement, la première fractale mathématique est la courbe
de Von Koch. Elle a été dessinée au début du siècle,
avant même d'être baptisée « fractale ». La courbe
est très simple à construire. Il suffit de dessiner un triangle
équilatéral (trois côtés de même longueur). Chaque
côté du triangle est divisé en trois tiers. Le tiers du milieu
sert de base à un nouveau triangle équilatéral, puis il est
effacé. On recommence la procédure sur chaque nouveau côté...
et ainsi de suite jusqu'à l'infini. La courbe est fermée, c'est-à-dire
qu'elle ne possède pas de « bouts » libres, et pourtant elle
est de longueur infinie ! Une bien étrange propriété...
Autre caractéristique d'une fractale : sa dimension. Dans le monde qui nous entoure, nous avons l'habitude de considérer les objets comme des figures à zéro, une, deux, ou trois dimensions, selon qu'elles possèdent une longueur, une largeur et une épaisseur. Un point tracé au crayon ne possède ni longueur, ni largeur, ni profondeur : il est de dimension 0. Un trait possède une longueur, mais pas de largeur ni de profondeur : il est de dimension 1. Une feuille de papier est une surface à deux dimensions (on ne tient pas compte de l'épaisseur du papier). Un dé à jouer est de dimension 3. La courbe de Von Koch, quant à elle, se dessine à l'aide d'un seul trait de crayon. Sa dimension devrait donc être égale à 1. Pourtant, on pourrait presque considérer qu'elle possède une seconde dimension. Elle ressemble à un accordéon qu'on ne pourra jamais complètement déplier. La courbe de Koch se situe à mi-chemin entre une ligne simple et une surface. Mandelbrot lui attribue une nouvelle dimension, qu'il nomme fractale, et qu'il situe entre 1 (dimension d'une droite) et 2 (dimension d'une surface). Toutes les courbes fractales se voient attribuer ainsi une dimension fractale qui est non entière. 
|
|
Les références Up Page Réseau Pepe @rt Flash Cybersciences Dieu joue-t-il aux dés ? Ian Stewart Pour la Science avril / juin 2005 Mathématiques exotiques n°47 Science & Vie août 1999 n°995 Pourquoi ce site Je crois que, si les êtres humains que nous sommes ne parviennent pas toujours à évoluer comme ils le souhaiteraient _à s'épanouir professionnellement, sentimentalement et sexuellement (ce que j'appelle les trois pôles d'intérêts) c'est parce qu'il y a des barrages qui entravent leur désir d'accéder à un rêve inachevé. Je pars du principe que tout est possible, à condition de s'entourer de gens qui nous poussent à croire en nous. Contribuer au Réseau Pepe Ce site est avant tout une encyclopédie ouverte à l'imagination et au savoir, où chacun(e) d'entre vous peut participer. Si vous avez envie de partager une passion, ou si vous sentez le besoin de vous exprimer sur un point précis, je vous invite à m'adresser un e-mail (adresse électronique accessible sur ma page d'accueil). |
|
Mais encore … Up Page Ce que vous avez toujours voulu savoir La théorie des fractales permet d'expliquer certains phénomènes naturels, comme la pollution atmosphérique, formée d'agrégats qui s'assemblent de façon fractale. Les formes de Mandelbrot sont aussi liées à la théorie du chaos, qui essaie d'expliquer, par exemple, les phénomènes de la météo. Cycles fractales Yonathan Shapir et ses collègues de l’université de Rochester, suggèrent de remplacer dans les équations la variable représentant le temps par le nombre de cycle de croissance et de décroissance. Ce résultat a été confirmé par l’analyse des irrégularités d’une surface d’argent soumise à de nombreuses dépositions et dissolutions successives. Ces nouvelles équations fractales promettent donc d’ores et déjà de mieux évaluer le dosage des chimiothérapies, la durée de vie des batteries, mais aussi de prévoir l’évolution des populations de bactéries suivant des nutriments, ou la forme des côtes assaillies par les marées régulières. Chaos et fractals Des systèmes qui suivent des lois précises et simples peuvent parfois agir de manière aléatoire, inconstante et imprévisible. Un univers où rien n'est comme il semble, où les formes mathématiques familières comme l'ellipse et le cercle engendrent des structures infiniment complexes, que l'on nomme fractals. 
Fractales en zones urbaines africaines (Zambie & Zoulou) 
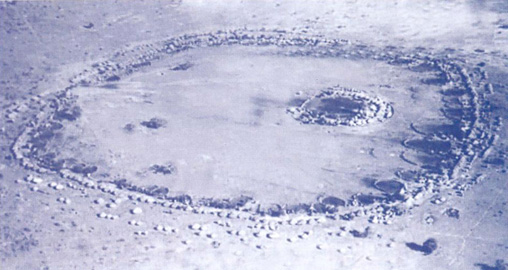
A droite, un village zoulou traditionnel, an Zimbabwe. A gauche, vue aérienne d'un village Ba-ila, en Zambie. Ci-après, la structure fractale du village Ba-ila. Le motif (a) est répété sur les segments qui le composent. A nouveau, l'opération est effectuée sur les mêmes zones du motif créé (b). Le résultat (c) est similaire à la vue d'ensemble du village. 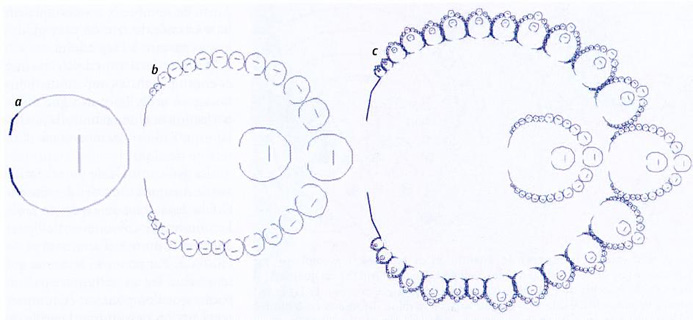
|