Equipotentielles La petite histoire Comprendre simplement Domaines de présence Son interprétation dans l'avenir Les références Mais encore …

by Pepe ©   Accueil  Arborescence  Page précédente

La petite histoire  Up Page Origine, raisons, hasard Il existe, en sciences physiques comme en cosmologie, nombre de domaines où les notions de lignes de champ et d'équipotentielles interviennent. Les lignes de champ sont pratiques lorsque il s'agit de les appliquer à des charges électriques immobiles ou à des objets massiques statiques dans l'espace, par exemple. Toutefois lorsqu'il va falloir appliquer la notion de lignes de champ à des particules en mouvement, le cerveau se heurte à une gymnastique d'esprit qui n'est pas souple et naturelle. La notion d'équipotentielle ouvre alors de plus belles perspectives et de liberté d'interprétations.

Comprendre simplement  Up Page Question d'interpétation La première étape consiste à se visualiser ce que sont des équipotentielles dans l'Univers des objets statiques. Ensuite, la deuxième étape aidera à se matérialiser l'utilité de passer aux équipotentielles, plutôt que de se cantonner aux lignes de champs.

Domaines de présence  Up Page Exemples de lignes de champ Charges ponctuelles identiques   Charges onctuelles oppossés   Charges ponctuelles (+1q) & (+4q)   Quatre charges ponctuelles sur un carré   Deux fils parallèles de même charge   Deux fils parallèles en opposition de charge   Deux fils parallèle de charge différente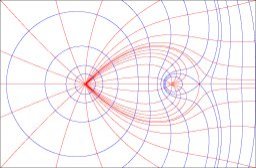

Son interprétation dans l'avenir  Up Page Monde futur Lorsque deux pierres rentrent en contact avec une étendue d'eau, ils se forment alors à la surface des ondulations et des interférences. Les formes géométriques qui découlent de la chute des pierres sur l'eau se trouvent être tout simplement des équipotentielles. Il est regrettable que l'être humain se soit focalisé et obstiné à des lignes de champ pour interpréter les phénomènes physiques qui l'entourent, car cette notion n'est pas naturelle. Pour preuve, la nature montre toujours des équipotentielles, et non des lignes de champs.

Les références  Up Page Réseau Pepe Source   Pourquoi ce site Je crois que, si les êtres humains que nous sommes ne parviennent pas toujours à évoluer comme ils le souhaiteraient _à s'épanouir professionnellement, sentimentalement et sexuellement (ce que j'appelle les trois pôles d'intérêts) c'est parce qu'il y a des barrages qui entravent leur désir d'accéder à un rêve inachevé. Je pars du principe que tout est possible, à condition de s'entourer de gens qui nous poussent à croire en nous.   Contribuer au Réseau Pepe Ce site est avant tout une encyclopédie ouverte à l'imagination et au savoir, où chacun(e) d'entre vous peut participer. Si vous avez envie de partager une passion, ou si vous sentez le besoin de vous exprimer sur un point précis, je vous invite à m'adresser un e-mail (adresse électronique accessible sur ma page d'accueil).

Mais encore …  Up Page Pourquoi avoir inventé les lignes de champ ? Il existe deux modes d'interprétations: 1° Voyager au moyen d'un bateau sur une trajectoire sinueuse, qui se trouve être perturbée par la chute de deux pierres, c'est comme être sur une ligne de conduite (ou ligne de champ). 2° Disposer une multitude d'objets sur l'eau est regarder leur évolution quand deux pierres viennent perturber la surface de l'eau, c'est suivre des ondulations cohérentes et régulières. Les ondes se perdent à l'infini, tant dans leur forme rigoureuse que dans leur amplitude, mais l'image des équipotentielles est plus parlante que celles des lignes de champ.   Notion de fonctions Il existe une infinité de fonctions mathématiques caractérisant le déplacement d'un point M de coordonnées (x,y) sur une ligne de conduite (ou ligne de champ). En revanche, il est facile d'avoir qu'une seule fonction mathématique  schématisant l'évolution des équipotentielles qui partent du centre vers l'infini. A chaque couple de valeur (x,y) d'un point M, il est possible de construire une courbe fermée (ou équipotentielle) indiquant sur quelle isovaleur la particule peut se trouver.