Attracteurs chaotiques La petite histoire Comprendre simplement Domaines de présence Son interprétation dans l'avenir Les références Mais encore …

by Pepe ©   Accueil  Arborescence  Page précédente

La petite histoire  Up Page Attracteurs de Lorentz

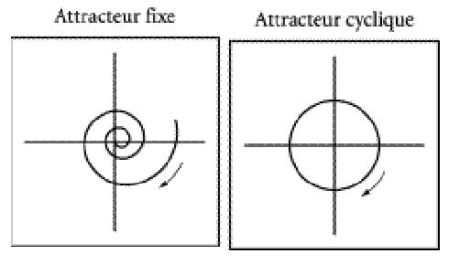
Comprendre simplement  Up Page Systèmes instables Systèmes chaotiques Une catégorie importante de systèmes instables est formée par les systèmes dits "chaotique", dans lesquels deux trajectoires aussi voisines que l'on veut à l'instant initial divergent exponentiellement avec le temps.

Domaines de présence  Up Page Trajectoire d'un pendule elliptique Les courbes engendrées par une pointe suspendue à un pendule elliptique, comportent un "motif" initial qui se reproduit ensuite à une rotation près et avec un  léger amortissement, ce qui explique les spirales sur lesquelles se trouvent les pointes homologues.

Son interprétation dans l'avenir  Up Page Attracteur de Lorenz dans l'espace des phases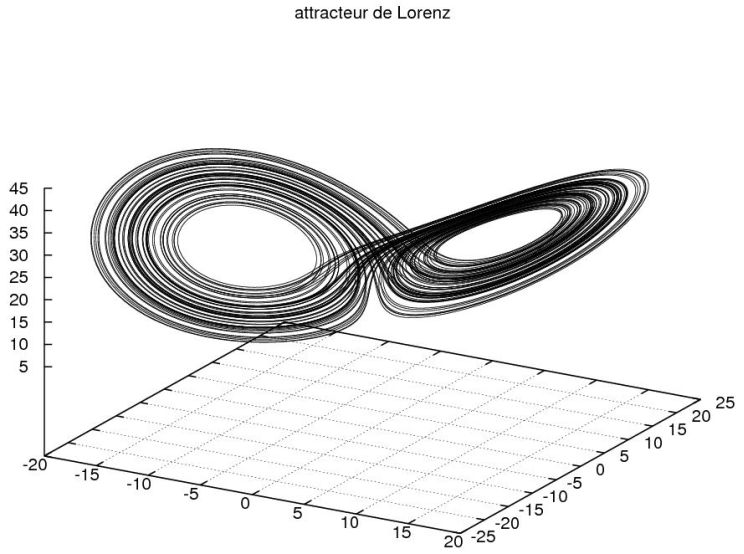

Les références  Up Page Réseau Pepe Lois du chaos Ilya Prigogine Science & Vie mars 1944 n°319   Pourquoi ce site Je crois que, si les êtres humains que nous sommes ne parviennent pas toujours à évoluer comme ils le souhaiteraient _à s'épanouir professionnellement, sentimentalement et sexuellement (ce que j'appelle les trois pôles d'intérêts) c'est parce qu'il y a des barrages qui entravent leur désir d'accéder à un rêve inachevé. Je pars du principe que tout est possible, à condition de s'entourer de gens qui nous poussent à croire en nous.   Contribuer au Réseau Pepe Ce site est avant tout une encyclopédie ouverte à l'imagination et au savoir, où chacun(e) d'entre vous peut participer. Si vous avez envie de partager une passion, ou si vous sentez le besoin de vous exprimer sur un point précis, je vous invite à m'adresser un e-mail (adresse électronique accessible sur ma page d'accueil).

Mais encore …  Up Page Ce que vous avez toujours voulu savoir