Accueil Arborescence Page précédente


|
by Pepe © Accueil Arborescence Page précédente |


|
|
La petite histoire Up Page Les Maîtres du Temps Les Mayas étaient passés maîtres dans l'art de manipuler les calendriers et utilisaient des sortes d'algorithmes pour calculer dates et durées. 
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Comprendre simplement Up Page Richesse du peuple maya Les Mayas ont culturellement dominé un immense territoire au Sud du Mexique jusqu'à la conquête espagnole au XVIe siècle. Cette civilisation vivait principalement du maïs, plusieurs siècles avant notre ère, et, dès les premièrs siècles de notre ère, construisait des pyramides, inventait son écriture. 
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Domaines de présence Up Page Palenque En 1746, le père de Solis est envoyé avec sa famille par son évêque à Santo Domingo de Palenque. A la recherche de terres à cultiver, ils redécouvrent en forêt des "maisons de pierre" abandonnées depuis des siècles: ils sont les premiers à pénétrer sur un site maya. En 1787, de retour de Palenque, Antonio del Río rédige un rapport qui contient de nombreux plans et mesures de monuments. Parmi les opinions suscitées, l'une d'elles veut que la splendeur même des monuments prouve la venue, des Romains chez les Indigènes. En 1836, l'avocat américain John Lloyd Stephens rencontre le dessinateur anglais Frederick Catherwood et partent tous les deux au Yucatán, à contre-courant de la mode de l'époque, toute entière tournée vers les anciennes civilisations du Bassin méditerranéen que l'on vient de découvrir. En juillet 1840, les deux hommes repartent pour New York. Stephens y publie en 1841 ses Incidents of Travel in Central America, Chipias and Yucatán. Le livre fait sensation. Les deux hommes révèlent au grand public la civilisation maya avec son architecture, ses sculptures, ses fresques, ses stèles, son écriture. 
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Son interprétation dans l'avenir Up Page Les premiers déchiffrements Le codex Tro-Cortesianus (ici les pages 103 et 104) conservé à Madrid. Sur cet almanach lié à l'apiculture (les abeilles sont en rouge), les dates indiquées par des points et des barres sont celles du calendrier religieux, nommé tzolkin. 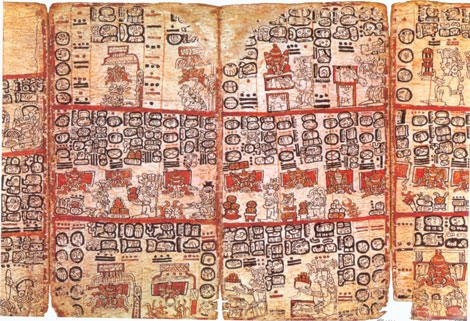
Le déchiffrement de l'écriture maya, à commencer par celui des dates et des durées des textes astronomiques. Les premiers travaux révèlent que les Mayas utilisèrent un système d'unités de temps et deux types de numération, de caractère vigésimal, c'est-à-dire en base 20: il comprend une unité principale, le tun (une année de compte de 360 jours, ou parfois de 400 jours), ses multiples, tels le katun (20 tun), le baktun (400 tun ou 20 katun), etc., et deux sous-multiples, le uinal (mois ou 1/18e de tun) et le kin (jour ou 1/20e de uinal ou 1/360e de tun). L'une des deux numérotations est positionnelle et ne note que les chiffres, l'autre est dispositionnelle et faut suivre chaque chiffre de l'indication de l'unité qu'il détermine. Les numérotations des deux types marquent les zéros, tant en position finale qu'en position intérieure. Le seul usage savant massivement attesté des numérotations mayas est la notation des dates et des durées. De ce point de vue, les Mayas se distinguent des Incas dont les quipus servaient de registres pour l'administration de l'empire. Les monuments et les codex montrent ces connaissances numériques à l'œuvre dans les calendriers et les éphémérides des principales planètes visibles à l'œil nu. 
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Les références Up Page Réseau Pepe Pour la Science avril / juin 2005 Mathématiques exotiques n°47 Pourquoi ce site Je crois que, si les êtres humains que nous sommes ne parviennent pas toujours à évoluer comme ils le souhaiteraient _à s'épanouir professionnellement, sentimentalement et sexuellement (ce que j'appelle les trois pôles d'intérêts) c'est parce qu'il y a des barrages qui entravent leur désir d'accéder à un rêve inachevé. Je pars du principe que tout est possible, à condition de s'entourer de gens qui nous poussent à croire en nous. Contribuer au Réseau Pepe Ce site est avant tout une encyclopédie ouverte à l'imagination et au savoir, où chacun(e) d'entre vous peut participer. Si vous avez envie de partager une passion, ou si vous sentez le besoin de vous exprimer sur un point précis, je vous invite à m'adresser un e-mail (adresse électronique accessible sur ma page d'accueil). 
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Mais encore … Up Page Le système point-barre Le système point-barre, attesté quatre ou cinq siècles avant notre ère, était utilisé par les Mésoaméricains pour noter les nombres de 1 à 19. 

|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Ce que vous avez toujours voulu savoir Up Page Dates et durées Le système "point-barre", caractéristique des cultures mésoaméricaines, était déjà connu des Olmèques, mais ne sera pas utilisé par les Aztèques. Nous savons par les Livres de Chilam Balam, rédigés en 1793 par un indigène acculturé, que les Mayas utilisaient des points et des barres pour représenter les entiers de 1 à 13, et aussi que l'année était une unité principale de mesure de temps. A la fin du XIXe siècle, Ernest Förstemann décrit précisément l'usage de ces chiffres dans la notation des très nombreuses dates et durées du codex de Dresde. Il remarque que la couleur est utilisée pour différencier les nombres selon qu'ils représentent des dates, écrites en rouge, ou des durées, écrites en noir. Par exemple, dans l'un des nombreux almanachs du codex de Dresde, on trouve la série: 13-Ahau +9 9-Muluc +11 7-Ahau +G 1-Ahau +10 11-Oc +15 13-Chicchan +9 9-Ix +11 7-Chicchan +G 1-Chicchan +10 11-Men +15 13-Oc +9 9-Cauac +11 7-Oc +G 1-Oc +10 11-Ahau +15 13-Men +9 9-Kan +11 7-Men +G 1-Men +10 11-Chicchan +15 13-Ahau. Förstemann découvre que de telles séquences représentent un cheminement dans le temps: partant d'une date origine 13-Ahau, on arrive en neuf jours (+9) à la date 9-Muluc, de là, en 11 jours (+11), on arrive à la date 7-Ahau, puis en 20 jours (noté G) à la date 1-Ahau, etc. Ce cheminement dans l'almanach fait parcourir exactement une année religieuse, nommée tzolkin, de 260 jours, selon un parcours en quatre étapes de 65 jours, chacune étant décomposée en pas de 9, 11, 20, 10 et 15 jours. En remarquant que 9+11=20 et que 10+15=20+5, on peut supposer que les différents pas de déplacement dans cet almanach pourraient avoir été motivés par l'idée d'approcher au mieux le parcours dans l'année solaire de 18 mois de 20 jours, complétés par une période de 5 jours, nommée Uayeb. On remarque aussi que les rangs des dates enregistrées par le scribe se déduisent les uns des autres par une addition modulo 13 (7+20=1, 1+10=11, 11+15=13), et que les noms des jours se déduisent par une addition modulo 20 (Ahau + 20 = Ahau). 
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Ce que vous avez toujours voulu savoir Up Page Les opérations mayas Ceci est lié à la nature des dates mayas: les 20 jours (ordonnés) X de l'année religieuse sont affectés d'un rang α variant de 1 à 13, de sorte que chacune des 260 dates religieuses est de la forme αX. On en déduit que +13 (respectivement +20) opère comme une translation qui laisse invariants les rangs α d'une date religieuse (respectivement, les noms de jours). Dans ce contexte des almanachs, le glyphe noté ici G représente le nombre 20. Fournissant un nouveau nombre d'appui additif, ce symbole étend, de façon similaire au rôle que jouent les chiffres X et C de la numérotation romaine, la capacité du système "point-barre", et permet d'écrire des nombres supérieurs à 20. Pour représenter les nombres de 21 à 39, les scribes préfixaient l'un des 19 chiffres "point-barre" au glyphe G, que l'on lisait uinic "homme" ou kal "vingtaine". On savait, notamment par l'oeuvre de Landa, que les numérotations mayas, parlées et écrites, sont toutes de caractère vigésimal. Förstemann montra que les 19 signes précédents, écrits en morphologie "point-barre", étaient utilisés, en dehors des almanachs, pour noter les chiffres des nombres représentant de grandes et très grandes durées, et que, dans cet usage, les Mayas avaient ajouté un 20e signe, un zéro, cardinal, le plus souvent écrit en rouge dans les codex. Ces 20 chiffres (de 0 à 19) étaient utilisés, comme le font toutes les numérotations vigésimales de position, pour représenter des nombres et ainsi effectuer des calculs arithmétiques et/ou mettre en évidence les résultats obtenus. Prenons par exemple la page 24 du codex de Dresde. Outre une table de 16 multiples de 2920 (cinq fois 584, nombre de jours de l'année vénusienne) et de quatre multiples de 260, cette page comprend, en bas à gauche, dans trois colonnes adjacentes, les chiffres formant les trois nombres - 6.2.0., 9.9.16.0.0. et 9.9.9.16.0. Ces nombres vigésimaux se transposent mécaniquement en numération décimale (6.2.0.= 6x360 + 2x20+0 = 2200; 9.9.16.0.0.= 9x144000 + 9x7200 + 16x360 + 0x20 + 0 = 1366560; 9.9.9.16.0 = 9x144000 + 9x7200 + 9x360 + 16x20 + 0 = 1364360). Ils sont reliés par une relation simple: le troisème est la différence du deuxième et du premier 9.9.9.16.0. = 9.9.16.0.0. + 6.2.0. ( 1364360=1366560-2200). 
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Ce que vous avez toujours voulu savoir Up Page Les deux calendriers mayas Le calendrier religieux, nommé Tzolkin, est fondé sur deux cycles, l'un de 13 rangs ou numéros matérialisés par un nombre de 1 à 13, l'autre de 20 noms de jours. Le calendrier civil, nommé haab, est constitué de 18 "mois" de 20 jours et d'une période de cinq jours, l'Uayeb. Les deux calendriers se combinaient et une date s'exprimait sous la forme αXβY, où α est le coefficient (entre 1 et 13), X est le jour religieux, β le quantième (entre 0 et 19, ou entre 0 et 5 pour l'Uayeb) et Y le mois civil. 
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Ce que vous avez toujours voulu savoir Up Page

|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Stèle de Quirigua Up Page Les deux syntaxes Les très nombreux exemples contenus dans le codex de Dresde ont confirmé l'hypothèse, jamais démentie, que cette numération est une numération de position. Cependant, le choix d'une année de compte de 360 jours (18 mois de 20 jours) fit couler beaucoup d'encre, et il conduit encore certains auteurs à ne pas reconnaître pleinement aux Mayas l'honneur d'avoir inventé une véritable numération de position, avec un zéro qui ne provient pas d'un blanc de séparation. Retenons un point jamais souligné, mais remarquable pour l'histoire comparée des numérations écrites de position: les scribes mayas utilisèrent de façon pertinente les deux dimensions de la page d'écriture. Ils le firent en distinguant l'espace (horizontal) de séparation des constituants d'un chiffre, et l'espace (vertical) de séparation des constituants d'un nombre. En contexte maya, on ne confond jamais les nombres .. "deux", et : "vingt et un". Les résultats obtenus furent utilisés pour déchiffrer les inscriptions monumentales. A l'inverse des codex, les stèles et les monuments représentent les durées comme des nombres-de, c'est-à-dire par des notations où les chiffres sont systématiquement suivis du nom des unités qu'ils dénombrent: par exemple, 9- baktun 17- katun 0- tun 0- uinal 0- kin, sur la stèle de Quirigua (voir la figure ci-dessous), et non pas 9.17.0.0.0. comme il serait écrit dans un codex. Cette durée équivaut à 1 418 400 kins, ou jours Les constituants numériques sont écrits dans l'ordre décroissant (plus rarement croissant) des glyphes de période ou unités de temps, et les zéros, redondants dans ce type de système dit "de disposition", sont néanmoins toujours écrits, tant en position finale qu'en position intérieure. Les scribes utilisaient, outre les chiffres "point-barre", un second jeu de chiffres faits de têtes dites "glyphes céphalomorphes". La plupart des durées étaient représentées par des nombres à cinq chiffres commençant par un 9 (quatre points et une barre) ou par une tête "barbue". Ce glyphe céphalomorphe devait être le 9 du second jeu de chiffres. De façon exceptionnelle, les Mayas représentèrent les coefficients des unités de temps par des personnages entiers. Ce système ne diffère pas fondamentalement de celui des chiffres céphalomorphes, et, malgré sa rareté, son déchiffrement n'a pas posé de difficultés. A l'instar du système positionnel, d'innombrables vérifications confirmèrent les hypothèses de déchiffrement des durées notées en systèmes dispositionnels, de style normal et de style céphalomorphe. 
La date de construction de la stèle de Quirigua. Après un glyphe introductif (a) qui indique le mois d'érection, on lit sur les cinq premiers glyphes (b) le nombre de jours écoulés depuis le début de l'ère maya, comptés en années de 360 jours et en base 20: 9 baktun 17 katun 0 tun 0 uinal 0 kin (soit 1 418 400 jours). Il s'agit d'une numération de disposition, mais qui comprend un zéro (cardinal). On lit aussi la date (c) du calendrier religieux (13 Ahau), et la date du calendrier civil (d) indiquée en bas (18 Cumhu); des dates que l'on aurait pu déduire des glyphes précédents.

|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Ce que vous avez toujours voulu savoir Up Page Les calendriers Comme leurs voisins mésoaméricains, les Mayas connaissaient une année de 260 jours, dite année religieuse ou tzolkin. Chaque jour était désigné par une expression de la forme αX, faite d'un rang α et d'un nom X de jour, obtenue par produit de deux cycles. Les rangs α sont les entiers de 1 à 13. Les noms de jour constituent un cycle de 20 éléments. Comme nos lundi 3, mardi 4, mercredi 5, les rangs et les noms progressent tous deux d'une unité lorsque l'on passe du jour au lendemain. Les Mayas disposaient aussi d'une année de 365 jours, dite année solaire ou haab. Elle comprend 18 mois de 20 jours, et une période complémentaire de 5 jours nommée Uayeb. Chaque jour de l'année solaire était désigné par une expression de la forme βY (constituée d'un rang β et d'un nom Y de mois) obtenue par produit de deux cycles. Les rangs β des jours sont les entiers de 0 à 19, les rangs des jours de la période Uayeb sont les entiers de 0 à 4. Les noms des 18 mois plus celui de la période complémentaire forment un cycle de 19 éléments. Comme nos 3 juillet, 4 juillet ..., les rangs progressent d'une unité tant que l'on reste dans le même mois, sinon le rang passe à zéro et le nom de mois est remplacé par le suivant dans la liste. Une date maya se présente ainsi sous la forme αXβY obtenue par produit des années religieuse et solaire, par exemple 4 Ahau 8 Cumku. La date du lendemain sera 5 Imix 9 Cumku. La coordination des années religieuse αX et solaire βY est caractéristique du génie maya. Le produit αXβY est lui-même un nouveau cycle, une sorte de super-année de 18 980 jours (le plus petit multiple commun à 365 et 260 jours) qui s'exprime facilement en années. On parle de Calendar Round, égal à 52 années solaires et à 73 années religieuses. Lorsque l'on dispose d'une date origine, on peut identifier date et durée. La date origine des Mayas était un 4 Ahau 8 Cumku. La plupart des spécialistes s'accordent pour dire que cette origine, aussi 13.0.0.0.0., correspond au 13 août 3114 avant notre ère. Une date pouvait donc aussi être notée comme une durée. Même si 9.1.0.0.0. est une date moins parlante que 6 Ahau 13 Yaxkin, cette date a l'avantage d'être "absolue"; la date 6 <Ahau 13 Yaxkin est "relative" pour n'être définie qu'à un nombre entier de Calendar Round près. Les transpositions d'un système de datation à l'autre se font mécaniquement. Il s'agit d'un problème de comput que les scribes résolurent ..., mais l'histoire ne nous a pas fait parvenir les algorithmes qu'ils utilisaient. Etant tous les deux inférieurs à 20, la notation des rangs alpha et beta d'une date ne nécessite que la connaissance des chiffres de la numération vigésimale. Les Mayas ont utilisé tous les styles présentés précédemment, c'est-à-dire les morphologies "point-barre", céphalomorphe et anthropomorphe. A une exception près, le zéro des dates solaires: alors que le chiffre zéro cardinal (celui des durées) existe, les Mayas ne l'ont pas utilisé pour représenter les dates de l'année solaire dont le coefficient beta est un zéro ordinal qui indique le rang. Le zéro de la date 0 Pop n'est jamais représenté par le même glyphe que le zéro des durées (par exemple, le zéro de 0 Uinal) et ceci tant dans les codex que sur les stèles et les monuments. Ainsi, les Mayas distinguèrent les faces ordinale et cardinale du nombre (les deux zéros mayas). Nous avons décrit les numérations de type positionnel et dispositionnel, dans les styles "point-barre", céphalomorphe et anthropomorphe. Dans tous les cas, une durée d est représentée par un nombre (ou un nombre-de) qui s'analyse comme une somme ordonnée de produits que représente la formule d=σciPi. Dans cette formule, ci représente un coefficient toujours marqué en maya par un chiffre, et Pi une unité ou période de temps; les Pi marqués par un glyphe de période dans les systèmes dispositionnels, mais, en numération de position des codex, ils ne le sont pas (ils sont seulement marqués par la position des ci). En convenant que les parenthèses représentent un élément facultatif, la formule σciPi résume toute la "syntaxe" des systèmes mayas de notation des durées ou des nombres. Dans Relación de las cosas de Yucatán, Diego de Landa rapporte également une figure nommée Girra de los Katunes, ou Roue des katuns qui montre une suite de date progressant par pas de 20 ans ou de un katun: Ahau XI Buluc Ahau; Ahau IX Bolon Ahau, etc. Outre la capacité de synthétiser les informations, la figure prouve que les scribes maîtrisaient les effets d'une translation temporelle. Ils savaient, par exemple, que tout déplacement d'un katun laisse invariant le nom des jours religieux (ici, le nom Ahau) et fait reculer le rang de deux unités (11, 9, 7 ...). 
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Ce que vous avez toujours voulu savoir Up Page Le savoir des scribes L'analyse de ce condensé de résultats a permis à Goodman d'énoncer plusieurs hypothèses. L'une d'elle stipule que l'année dont traite le Roue des katuns n'est ni l'année religieuse de 260 jours ni l'année civile de 365 jours: les déplacements par 20x260 et 20x365 jours ne font pas reculer de deux le rang alpha du jour invariant Ahau. Pour cela, il faut une année de x jours, telle que 20x=-2 (modulo 13). Le petit x qui convient est 360. Dès lors, un katun est égal à 7 200 jours. Tout déplacement de 7200 jours laisse Ahau invariant (7200=0mod20) et fait reculer alpha de deux rangs (7200=-2mod13). Nous avons vu que tout almanach est une suite alternée de dates et de durées. On trouve aussi dans les codex un autre type de tableaux où, à l'inverse des almanachs, le scribe semble ne pas indiquer les durées qui séparent les dates. Ainsi, la page 32a du codex de Dresde (figure ci-dessous) contient un tableau de quatre colonnes et cinq lignes, soit 20 cellules contenant chacune un nom de jour. Au-dessus, figurent cinq occurrences du nombre 13: c'est le rang alpha des 20 jours du tableau. Les dates se succèdent en fonction d'une loi à découvrir qui dépend de l'ordre de lecture adopté. Le calcul montre qu'elles sont équidistantes, et forment une progression de raison 169 jours (lecture par ligne, de gauche à droite) ou 156 jours (par colonne, de haut en bas). Selon un autre ordre de lecture (des déplacements rétrogrades), les dates sont en progression de 91 jours (lecture par ligne), ou de 364 jours (lecture par colonne). Comment choisir ? Visiblement, le tableau dit que ces valeurs laissent invariant le rang 13, et précise comment varie le nom du jour. Mais il y a plus. La valeur 364, en effet, appelle son successeur 365, lequel évoque inévitablement l'année solaire. En d'autres termes, à une unité près, le haab est divisible par 13. Un scribe savait-il cela ? Oui, s'il utilisait l'ordre de lecture qui distingue les nombres 91 et 364. Ces nombres sont parlants pour un scribe, puisque 364 est l'année zodiacale des 13 signes-constellations de 28 jours chacune. C'est propablement l'ordre canonique de lecture, et l'on peut admettre que les scribes distinguaient ces deux valeurs. L'ensemble des tableaux de dates et des tables de multiples semble être un algorithme grâce auquel le scribe définissait les dates images de translations de pas de 91 jours, de 364 jours ou de n'importe quelle combinaison des multiples de ces deux pas. Toutes ces translations laissent le rang invariable. Quels problèmes ces outils servaient-ils à résoudre ? 
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Ce que vous avez toujours voulu savoir Up Page Codex Dresde: page 32A La page 32A du Codex Dresde contient un tableau (en rouge) que les scribes utilisaient comme table de multiples de 91 et 364 jours. Ces nombres correspondent au pas de lecture case à case quand on lit le tableau respectivement par lignes et par colonnes selon une lecture rétrograde, c'est-à-dire de droite à gauche et de bas en haut. Voici la lecture correspondante: Manik Cib Chicchan Ix Chuen Ahau Muluc Etznab Men Kan Ben Ik Cauac Lamat Caban Cimi Akbal Eb Imix Oc 
Le texte de la stèle 3 de Piedras Negras, au Guatemala, dit que la reine Katun Ahau est née un 5 Cib 14 Yaxkin, que 12-tun 10-uinal 0-kin ont passé jusqu'à son mariage, et encore 1-katun 1-tun 11-uinal 10-kin jusqu'à la naissance de la princesse Kin Ahau. Le scribe était donc capable de calculer ou de vérifier qu'une date est bien l'image d'une autre par une translation et de dire combien de jours séparent deux dates données. C'est le premier problème de l'arithmétique maya. Il consiste à déterminer la date alpha'X'beta'Y', connaissant la distance σciPi, qui la sépare d'une date alphaXbetaY donnée. Pour les durées inférieures à une année, il suffit de lire le calendrier, ou connaître la succession des constituants alpha, X, beta et Y des dates. Pour des durées plus importantes, il faut recourir au calcul. 
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Ce que vous avez toujours voulu savoir Up Page Deux problèmes de l'arithmétique maya Les algorithmes sous-jacents aux tableaux de dates et aux tables de multiples illustrent vraisemblablement les méthodes de résolution de ces problèmes dans le cas des grandes durées. Ces méthodes étaient probablement fondées sur la connaissance des durées qui laissent invariantes tout ou partie d'une date. Le Calendar Round et ses multiples jouissent de cette propriété. La Roue des katuns laisse le nom du jour invariant et rétrograde son rang de deux unités. Le tableau de dates précédent dit que les rangs alpha sont invariants par translation de 364 jours, et que les noms de jour avancent de 4. Qu'ils aient mis ces propriétés en tableau prouve que les scribes connaissaient de telles modifications ou de telles invariances, et ceci pour toutes sortes de cycles. Et que ces connaissances permirent sans doute aux scribes de trouver, par exemple, l'image de la date donnée. Un deuxième type de problème consiste à déterminer la distance σciPi qui sépare deux dates données alphaYbetaY et alpha'X'betaY'. Sa difficulté provient du fait que l'inconnue est une fonction (une translation) et non une image. Familiers de toutes sortes de cycles, les scribes ont certainement eu l'idée de décomposer la difficulté. Par exemple, la structure de produits de cycles du Calendar Round invite à décomposer en mouvement plus élémentaires la translation à découvrir, et à chercher à transformer séparément alphaX en alpha'X' et betaY en beta'Y'. De la même façon que pour lire un déplacement sur un quadrillage, on peut décomposer la translation inconnue en un mouvement dans l'année religieuse et un autre dans l'année civile. On est ainsi conduit à deux stratégies simples. On se déplace d'abord dans l'année religieuse par un mouvement dR faisant passer de alphaX à alpha'X', sans se préoccuper de la partir solaire. Ou bien, on commence par se déplacer dans l'année civile par un mouvement dS permettant de passer de betaY à beta'Y', sans se préoccuper de la partie religieuse. Dans les deux cas, le premier mouvement modifie la partie qui n'a pas été prise en considération. Ainsi, dS transforme la position betaY en beta'Y' et modifie corrélativement la partie alphaX qui devient alpha1X1; il reste à trouver un mouvement qui conserve beta'Y' et fait passer de alpha1X1 à alpha'X'. Soit le schéma de résolution: trouver dS et calculer alpha1X1 tels que alphaXbetaY+dS=alpha1X1beta'Y'. Ou bien, trouver dR et calculer alpha'X' tels que alpha1X1beta'Y' +dR=alpha'X'beta'Y'. Prenons un exemple: déterminons la distance d des dates 13 Ahau 18 Kankin et 8 Oc 13 Yax, disons à l'aide de la seconde stratégie. Pour trouver le premier mouvement, dS, on calcule (ou on lit sur un calendrier) la distance entre les dates solaires 18 Kankin et 13 Yax: dS=-4.5. (soit 85 jours) et donc alpha1X1=6 Men. Reste à déterminer dR, le déplacement dans l'année religieuse, laissant invariante la date civile 13 Yax et en même temps transformer 6 Men et 8 Oc. Par définition, les translations multiples d'une année (365 jours) laissent invariantes les dates solaires, tels 13 Yax. Le mouvement dR doit donc être multiple de 365. Comme pour le premier mouvement, le srcibe calcule la distance entre alphaX=13 Ahau et alpha'X'=8 Oc. Il trouve 15. Une table des multiples de 365 rappelle au scribe qu'une translation d'un an augmente alpha d'une unité et X de cinq. Il en déduit qu'une translation de 15 années augmente alpha de 15, et fait en même temps avancer X de 15 fois 5 places, c'est-à-dire de 15 (mod20). Le second mouvement est retrouvé, c'est dR=15.x1.0.5. Ce produit s'écrit 15.3.15. D'où la solution d=dS+dR=-4.5. + 15.3.15. = 14.14.10.. Pour le moins, nous devons prêter aux Mayas des techniques élaborées de comptage et de repérage à l'intérieur d'une forêt de cycles dont ils maîtrisaient à coup sûr les multiples combinaisons engendrant, par produit, des cycles de plus en plus grands. Nous pouvons aussi leur accorder la connaissance des principales propriétés d'invariance des divers constituants d'une date, et de nombreux raccourcis montrant comment se comporte tel élément d'une date sous un déplacement d'amplitude donnée. Et, bien sûr aussi, la connaissance du calcul (addition et soustraction) selon un modulo, voire des résultats généraux sur les translations opérant sur les dates. Par ailleurs, une histoire comparée des numérations écrites ne peut ignorer que l'on assiste, chez les Mayas, à plusieurs innovations: l'invention "banale" d'un glyphe pour représenter le zéro cardinal, banale, car elle eut lieu aussi en Mésopotamie, en Inde et en Chine; l'invention "unique" d'un zéro "ordinal", spécialisé pour la notation du rang du premier/dernier jour d'une "treizaine" de dates de l'année religieuse; l'invention "étonnante" des glyphes de périodes pour représenter les unités successives du système des mesures du temps. L'étonnement provient du fait que des inscriptions plus anciennes, de type dispositionnel mais sans zéro, les notations olmèques, ne comportent pas de glyphes de période. André Cauty travaille au Centre d'Etude des Langues Indiennes d'Amériques (CNRS) à Villejuif. 
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||